CODEBUG (page 1)

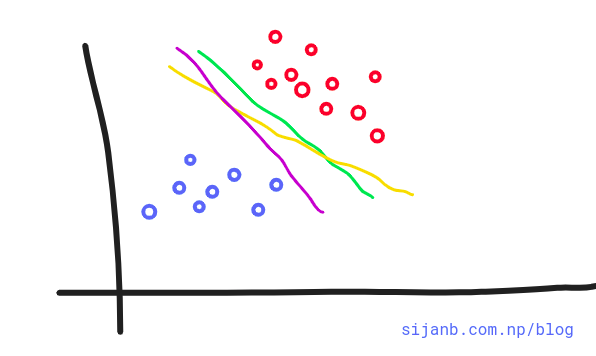
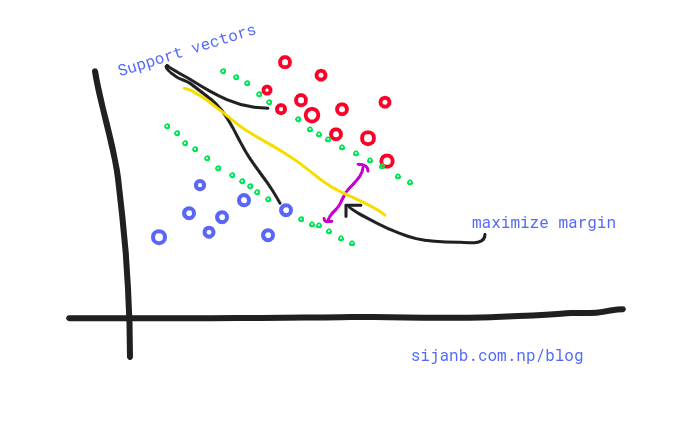
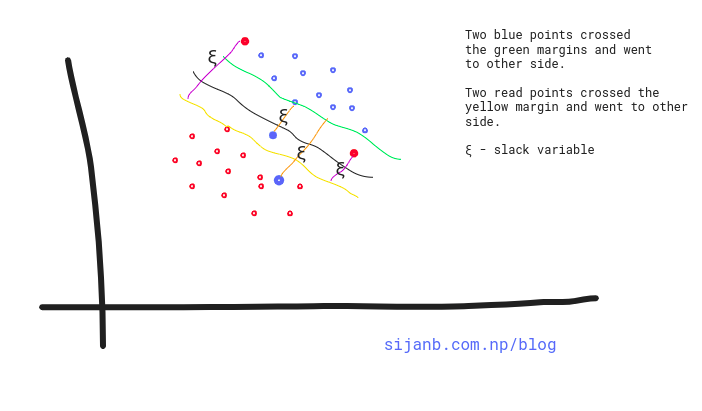
In this post, we will see how we can train support vector machines using stochastic gradient descent (SGD). Before jumping to the algorithm, we need to know why subgradients?

Here is a brief summary of the 0-1 loss and hinge loss:

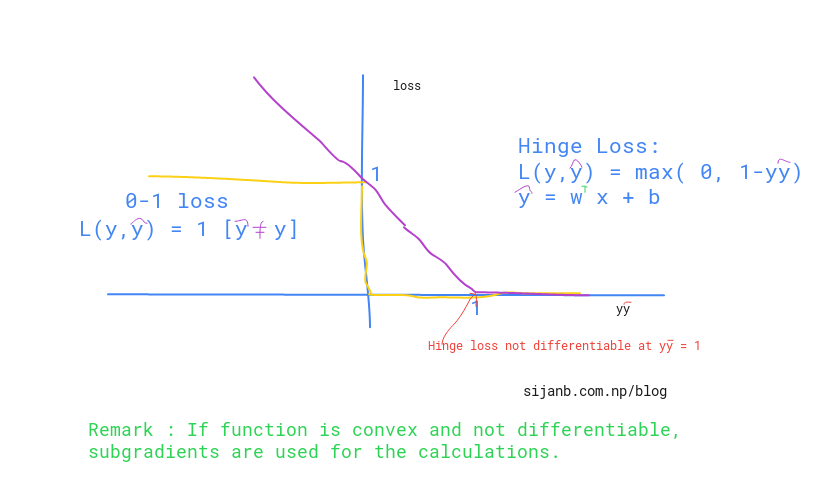
But, why don't we use 0-1 loss ?? The obvious reason is it is not convex. Another factor could be it's reaction to small changes in parameters. You can see from the graph, if you change (w,b) the loss will flip to either 0 or 1 very fast without acknowledging the in between values. The hinge loss,on the other hand, has smooth change until it reaches '1' along x-axis.

Support vector machine (SVM) is a supervised machine learning algorithm which is considered effective tool for both classification and regression problem.

In a simple word, SVM tries to find a linearly separable hyperplane in order to separate members of one class from another. If SVM can not find the hyperplane for a given data set, it applies non-linear mapping to the training data and transform them to higher dimension where it searches for the optimal hyperplane. The SVM algorithm uses support vectors and margins in order to draw these hyperplanes in the training data.

Since it has ability to understand the complex relation in input data by applying nonlinear mapping, it has high accuracy compare to other supervised classification algorithms (kNN, NCC..)

People have been using SVM for different applications like : text data classification, image data(handwritten) recognition and more.

Intuition:

Let us see a linearly separable problem as shown in the diagram below.

In the given diagram, we can draw infinite lines that can separate data into two different classes.

Can you decide Which of the lines (pink, yellow, green) better suits our problem? If you look closely, the green line is close to red dots and any minor change in data point may caues this point to fall into other class. On the other hand, Pink line is close to blue dots and similarly, a minor twist on data are prone to change the class of new point to other side and may misclassified.

But, the yellow line looks more stable, in the sense, it is far from data points on either side and not susceptible to the small changes in data observations.

Support vector machines help us to make a decision on this problem. If you think 'yellow' line in the figure is the optimal hyperplane for this problem, we can take this as an intuition that an optimal choice from the number of choices of hyperplanes is the one which is farthest from our training data points.

We can compute the perpendicular distances from all our training points to all possible hyperplanes and choose the one which has largest minimum distance to the training examples. The minimum distance between hyperplane and the observation point is called margin.

In summary, SVMs maximize the margin around our separating hyperplane. And, The idea is to draw a margin of some width around the separating hyperplane, up to the nearest point.

The training data that falls exactly on the boundaries of the margin are called

the support vectors. If these points shifted on any direction, they also influence the hyperplanes passing through the margin points and they also shifted. It is important to notice that support vectors are critical data points on our training set since they are the one defining margin boundaries.

It is important to note that the complexity of SVM is characterized by the number of support vectors, rather than the dimension of the feature space. That is the reason SVM has a comparatively less tendency to overfit.

Support vectors "support the plane" and are hence called Support Vectors.¶

Upto now, we are trying to find the hard-margin for our hyperplane. But, as shown in the diagram below, a single point can have high influence on our boundary. So hard margin SVM are sensitive to outliers, giving overfitted model.

What about we relax our hard margin condition? where, a small amount of data points are allowed to cross the margins/boundaries .i.e data points can be on incorrect side as well. This approach is called soft-margin. Soft in the sense that few data points can violate the margin condition. The softness is measured by slack variable; which control the position of training data points relative to the margins and our hyperplane. The ultimate goal is, our SVM tries to maximize the soft margin.

The Nearest centroid classifier (NCC) says that we should classify a data point to a class whose centroid is closest to this data point.

The algorithms follows:

Suppose $ c_l $ represents the set of indices which belong to class l. And n = |$c_l$|

1.Training step :¶

We compute the centroids(CTs) for each of the classes as:

$CT_l$ = $ \frac{1}{n} \sum_{i \in c_l} x_i $

2.Prediction step :¶

a. Given a new data point $x_{new}$, compute the distance between $x_{new}$ and each centroids as

distance : $|| x_{new} - $CT_l$||_2$ (Euclidean distance)

b. Assign the class to this new point which has minimum distance value.

Let us taken an example. We have to classify fruits into two classes : Apple and Orange, based on their height and width.

Our inputs (x) are :

x1=[5,6], x2=[5,7], x3=[4,3], x4=[5,7], x5=[6,4] and corrresponding labels (y) are

𝑦1='AP' 𝑦2='AP' 𝑦3='AP' 𝑦4='ORG' 𝑦5='ORG'

Here $x_i$ = [width, height] , 'AP' = 'Apple', 'ORG' = 'Orange'.

Now, centroids for two classes are :

$ CT_{AP} $ = $ \frac{1}{3} (5 + 5 + 4, 6 + 7 + 3) $ = ($\frac{14}{3}, \frac{16}{3} $)

$ CT_{ORG} $ = $ \frac{1}{2} (5 + 6, 7 + 4) $ = ($\frac{11}{2}, \frac{11}{2} $)

Suppose, you got a new test data point : (3, 7) i.e $x_{new}$, and you want to classify this point. We can calculate the distance between new point and our centroids as:

$ ||x_{new} - CT_{AP} || $ = || (3,7) - ($\frac{14}{3}, \frac{16}{3} $) || = 2.357

$ ||x_{new} - CT_{ORG} || $ = || (3,7) - ($\frac{11}{2}, \frac{11}{2} $) || = 2.915

Here, the new data point is classified as 'Apple' as the new data point is closest to the centroid of data points that belong to class 'Apple'

In this post, we are going to devise a measurement tool (perceptron model) in order to classify : whether a person is infected by a diseases or not.

In binary terms, the output will be { 1 if infected 0 not infected }

To build inputs for our neural network, we take readings from the patients and we will treat readings as follows :

  body temperature = {
                          1   if body temperator > 99'F
                         -1   if body temperator = 99'F
                     }
  
  heart rate = {
                      1   if heart rate > 60 to 100
                     -1   if heart rate = 60 to 100
                 }
  
   blood pressure = {
                          1   if heart rate > 120/80
                         -1   if heart rate = 120/80
                     }
 

So, input from each patient will be represented as a three dimensional vector:

  input = (body temperatur, heart rate, blood pressure)

So, a person can now be represented as : (1, -1, 1) i.e (body temperator > 99'F, heart rate = 60 to 100, heart rate > 120/80)

Let us create two inputs with desired output value

      x1 = (1, 1, 1), d1 = 1 (infected)
       x2 = (-1, -1, -1), d2 = 0 (not infected)

Let us take initial values for weights and biases: weights, w0 = (-1, 0.5, 0) bias, b0 = 0.5

And, activation function:

         A(S)   = {
                    1 if S >=0
                    0 otherwise
                  }

STEP 1¶

Feed x1 = (1, 1, 1) into the network.

weighted_sum:

S = (-1, 0.5, 0) * (1, 1, 1)^T + 0
  = -1 + 0.5 + 0 + 0
  = -0.5

When passed through activation function A(-0.5) = 0 = y1 We passed an infected input vector, but our perceptron classified it as not infected. Let's calculate the error term: e = d1 - y1 = 1 - 0 = 1 Update weight as:

             w1 = w0 + e * x1 = (-1, 0.5, 0) + 1 * (1, 1, 1) = (0, 1.5, 1)

And, update bias as: b1 = b0 + e = 1

STEP 2¶

Now, we feed second input (-1, -1, -1) into our network.

weighted_sum : S = w1 * x2^T + b1 = (0, 1.5, 1) * (-1, -1, -1)^T + 1 = -1.5 - 1 + 1 = -1.5 When passed through activation function A(-1.5) = 0 = y2 We passed an not infected input vector, and our perceptron successfully classified it as not infected.

STEP 3¶

Since, our first input is mis-classified, so we will go for it.

weighted_sum :

S = w1 * x1^T + b1 
  = (0, 1.5, 1) * (1, 1, 1)^T + 1
  = 1.5 + 1 + 1
  = 3.5

When passed through activation function A(3.5) = 1 = y3 We passed an infected input vector, and our perceptron successfully classified it as infected.

Here, both input vectors are correctly classified. i.e algorithm is converged to a solution point.

Deep learning, in simpler version is a learning mechanisms for Neural networks. And, Neural networks are computational model mimicing human nervous system which are capable of learning. Like interconnected neurons in human brains, the neural network is also connected by different nodes. It receives signals as a set of inputs, perform calcuations and signals output based on some activation value.

Here are some list of problems, that deep learning can solve

1. Classification : object and speech recongnistion, classify sentiments from text
2. Clustering : Fraud detection

Read more…