Before jumping to Gradient Descent, let's be clear about difference between backpropagation and gradient descent. Comparing things make it easier to learn !
Backpropagation :¶
Backpropagation is an efficient way of calculating gradients using chain rule.
Gradient Descent:¶
Gradient Descent is an optimization algorithm which is used in different machine learning algorithms to find parameters/combination of parameters which mimimizes the loss function.
** In case of neural network, we use backpropagation to calculate the gradient of loss function w.r.t to weights. Weights are the parameters of neural network.
** In case of linear regression, coefficients are the parameters!.
** Many machine learning algorithms are convex problems, so using gradient descent to get extrema makes more sense. For example, if you remember the solution of linear regression :
$ \beta = (X^T X)^{-1} X^T y $
Here, we can get the analytical solution by simply solving above equations. But, inverse calculation has $ O(N^3) $ complexity. It will be worst if our data size increases.
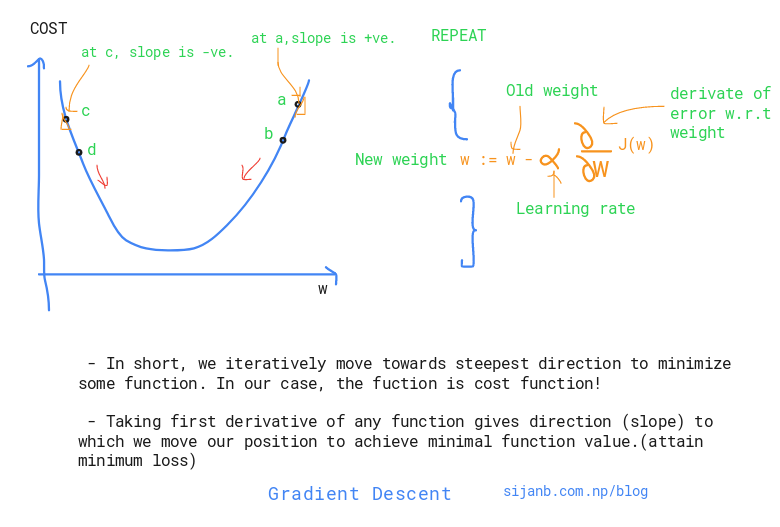
The algorithm has major three steps:
- Randomly select initial position (x) (e.g : setting initial weights/baises in neural network)
- Calculate derivative of the cost function (f) at that position, figuring out which direction we should move.
- Follow the direction, where the function is descending fastest, with small step of $ \alpha $ (learning rate)
if $ f^{'}(x) $ > 0 . f is increasing. so we have to move x to little left.
if $ f^{'}(x) $ < 0 . f is decreasing. so we have to move x to little right.
NOTE : If the derivative is +ve, it means the slope is going up when you move right so you have to descent to left. and if the derivative is -ve, it means the slope goes down when you move left so you need to descent to right.
So, at each position, we calcuate the derivative of the loss function to get the direction and move with a single step. But, how much is the ideal step size ? We have two different scenarios:
- If we set $\alpha$ to small, convergence will take longer.
- If we set $\alpha$ to large, algorithm might overshoot the minimum and jumps to-and-fro. So, algorithm might not be converging, in worst, it diverges from actual minimal.
Major Take-Aways
- Gradient descent is applied to minimize a function.
- Gradient descent will give optimal solution if the problem is convex.
- Using analytical solution could be computationally inefficient( e.g. linear regression), so applying Gradient descent on huge data sets is a good decision.
Just curious !
Can we still use gradient descent for non-convex problem and use the solution as a starting point or approximation?¶